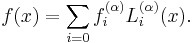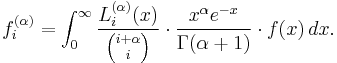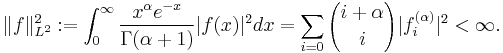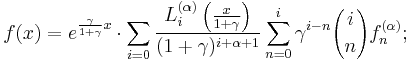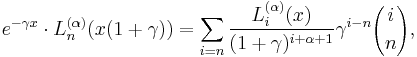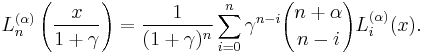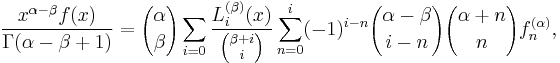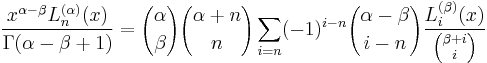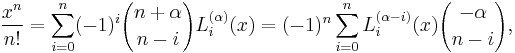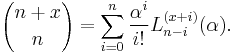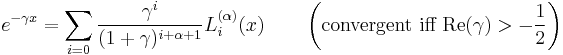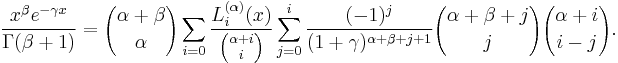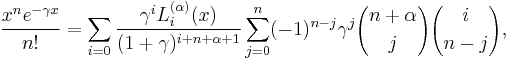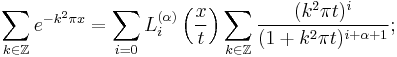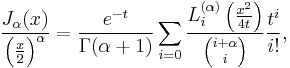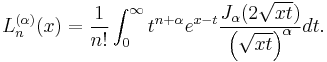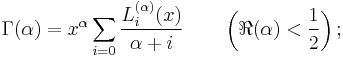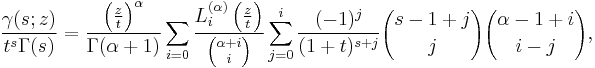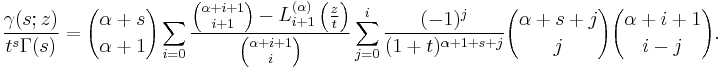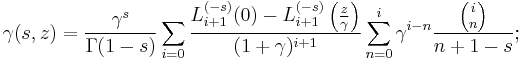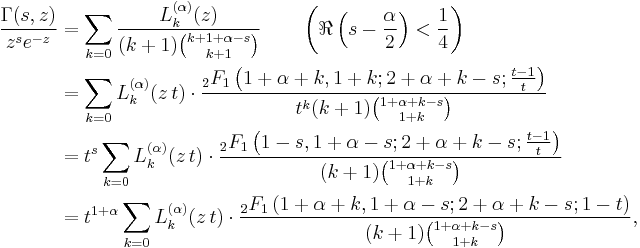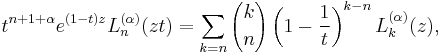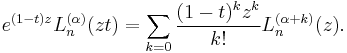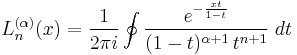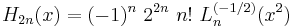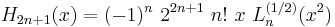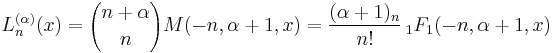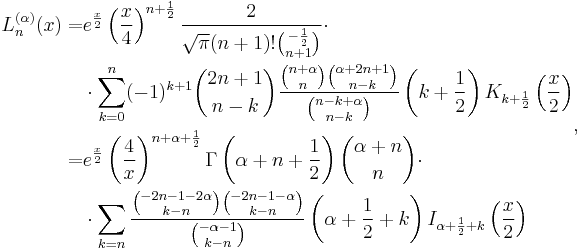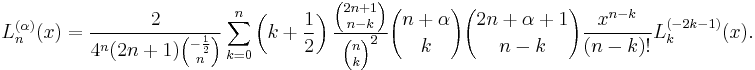Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre (1834 – 1886), are the canonical solutions of Laguerre's equation:
which is a second-order linear differential equation. This equation has nonsingular solutions only if n is a non-negative integer. The Laguerre polynomials are also used for Gaussian quadrature to numerically compute integrals of the form
These polynomials, usually denoted L0, L1, ..., are a polynomial sequence which may be defined by the Rodrigues formula
They are orthogonal to each other with respect to the inner product given by
The sequence of Laguerre polynomials is a Sheffer sequence.
The rook polynomials in combinatorics are more or less the same as Laguerre polynomials, up to elementary changes of variables.
The Laguerre polynomials arise in quantum mechanics, in the radial part of the solution of the Schrödinger equation for a one-electron atom.
Physicists often use a definition for the Laguerre polynomials that is larger, by a factor of n!, than the definition used here. (Furthermore, various physicist use somewhat different definitions of the so-called associated Laguerre polynomials, for instance in [Modern Quantum mechanics by J.J. Sakurai] the definition is different than the one found below. A comparison of notations can be found in [Introductory quantum mechanics by R.L. Liboff].)
Contents |
The first few polynomials
These are the first few Laguerre polynomials:
| n | 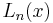 |
| 0 |  |
| 1 | 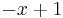 |
| 2 | 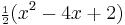 |
| 3 | 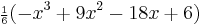 |
| 4 | 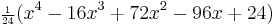 |
| 5 | 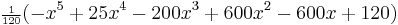 |
| 6 | 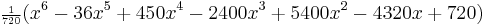 |
Recursive definition
We can also define the Laguerre polynomials recursively, defining the first two polynomials as
and then using the following recurrence relation for any k ≥ 1:
Generalized Laguerre polynomials
The polynomial solution of differential equation[1]
is called generalized Laguerre polynomials, or associated Laguerre polynomials. The Rodrigues' formula for them are
The simple Laguerre polynomials are recovered from the generalized polynomials by setting α = 0:
Explicit examples and properties of generalized Laguerre polynomials
- Laguerre functions are defined by confluent hypergeometric functions and Kummer's transformation as[2]
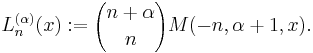
- When n is an integer the function reduces to a polynomial of degree n. It has the alternative expression[3]
- in terms of Kummer's function of the second kind.
- The generalized Laguerre polynomial of degree n is[4]
-
- (derived equivalently by applying Leibniz's theorem for differentiation of a product to Rodrigues' formula.)
- The first few generalized Laguerre polynomials are:
- The coefficient of the leading term is (−1)n/n!;
- The constant term, which is the value at 0, is
- Ln(α) has n real, strictly positive roots (notice that
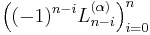 is a Sturm chain), which are all in the interval
is a Sturm chain), which are all in the interval ![\left( 0, n%2B\alpha%2B (n-1) \sqrt{n%2B\alpha} \right].](/2012-wikipedia_en_all_nopic_01_2012/I/687850c75046ae1294334e286885de3e.png)
- The polynomials' asymptotic behaviour for large n, but fixed α and x > 0, is given by
-
- and summarizing by
where 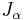 is the Bessel function.
is the Bessel function.
- Moreover
- whenever n tends to infinity.
Recurrence relations
Laguerre's polynomials satisfy the recurrence relations
and
in particular
and
or
moreover
They can be used to derive the four 3-point-rules
combined they give this additional, useful recurrence relations
A somewhat curious identity, valid for integer i and n, is
it may be used to derive the partial fraction decomposition
Derivatives of generalized Laguerre polynomials
Differentiating the power series representation of a generalized Laguerre polynomial k times leads to
moreover, this following equation holds
which generalizes with Cauchy's formula to
The derivate with respect to the second variable  has the surprising form
has the surprising form
The generalized associated Laguerre polynomials obey the differential equation
which may be compared with the equation obeyed by the k-th derivative of the ordinary Laguerre polynomial,
where 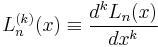 for this equation only.
for this equation only.
This points to a special case (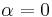 ) of the formula above: for integer
) of the formula above: for integer 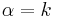 the generalized polynomial may be written
the generalized polynomial may be written 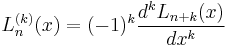 , the shift by k sometimes causing confusion with the usual parenthesis notation for a derivative.
, the shift by k sometimes causing confusion with the usual parenthesis notation for a derivative.
In Sturm-Liouville form the differential equation is
which shows that 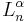 is an eigenvector for the eigenvalue
is an eigenvector for the eigenvalue  .
.
Orthogonality
The associated Laguerre polynomials are orthogonal over [0, ∞) with respect to the measure with weighting function xα e −x:[5]
which follows from
If 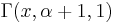 denoted the Gamma distribution then the orthogonality relation can be written as
denoted the Gamma distribution then the orthogonality relation can be written as
The associated, symmetric kernel polynomial has the representations (Christoffel–Darboux formula)
recursively
Moreover,
in the associated L2[0, ∞)-space.
Turán's inequalities can be derived here, which is
The following integral is needed in the quantum mechanical treatment of the hydrogen atom,
Series expansions
Let a function have the (formal) series expansion
Then
The series converges in the associated Hilbert space 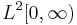 , iff
, iff
A related series expansion is
in particular
which follows from
Secondly,
a consequence derived from
for 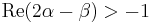 .
.
More and other examples
Monomials are represented as
binomials have the parametrization
This leads directly to
and, even more generally,
For  a non-negative integer this simplifies to
a non-negative integer this simplifies to
for 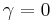 to
to
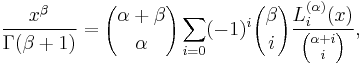 or
or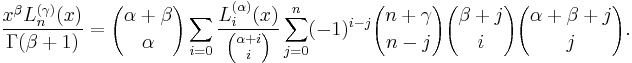
Jacobi's theta function has the representation
the Bessel function 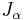 can be expressed (using an arbitrarily chosen parameter
can be expressed (using an arbitrarily chosen parameter  ) as
) as
and thus
Gamma function has the parametrization
the lower incomplete Gamma function has the representations
and
The upper incomplete gamma function then is
where 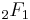 denotes the hypergeometric function.
denotes the hypergeometric function.
Multiplication theorems
Erdélyi gives the following two multiplication theorems [6]
As a contour integral
The polynomials may be expressed in terms of a contour integral
where the contour circles the origin once in a counterclockwise direction.
Relation to Hermite polynomials
The generalized Laguerre polynomials are related to the Hermite polynomials:
and
where the Hn(x) are the Hermite polynomials based on the weighting function exp(−x2), the so-called "physicist's version."
Because of this, the generalized Laguerre polynomials arise in the treatment of the quantum harmonic oscillator.
Relation to hypergeometric functions
The Laguerre polynomials may be defined in terms of hypergeometric functions, specifically the confluent hypergeometric functions, as
where 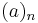 is the Pochhammer symbol (which in this case represents the rising factorial).
is the Pochhammer symbol (which in this case represents the rising factorial).
Relation to Bessel functions
In terms of modified Bessel functions (Bessel polynomials) these following relations hold:
or further elaborated
Notes
- ^ A&S p. 781
- ^ A&S p.509
- ^ A&S p.510
- ^ A&S p. 775
- ^ A&S p. 774
- ^ C. Truesdell, "On the Addition and Multiplication Theorems for the Special Functions", Proceedings of the National Academy of Sciences, Mathematics, (1950) pp.752-757.
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 22", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 773, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_773.htm.
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/18
- B Spain, M G Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 10 deals with Laguerre polynomials.
- Eric W. Weisstein, "Laguerre Polynomial", From MathWorld—A Wolfram Web Resource.
- George Arfken and Hans Weber (2000). Mathematical Methods for Physicists. Academic Press. ISBN 0-12-059825-6.
- S. S. Bayin (2006), Mathematical Methods in Science and Engineering, Wiley, Chapter 3.
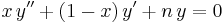
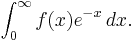
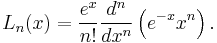
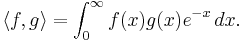
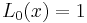

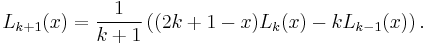
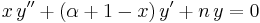
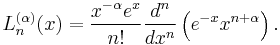
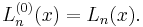
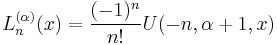
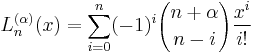
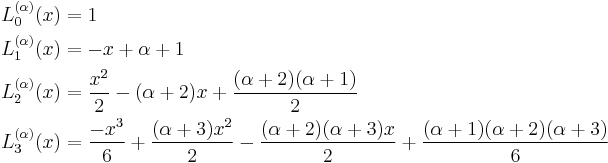
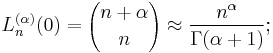
![L_n^{(\alpha)}(x) \approx \frac{n^{\frac{\alpha}{2}-\frac{1}{4}}}{\sqrt{\pi}} \frac{e^{\frac{x}{2}}}{x^{\frac{\alpha}{2}%2B\frac{1}{4}}} \cos\left[2 \sqrt{x \left(n%2B\frac{\alpha%2B1}{2}\right)}- \frac{\pi}{2}\left(\alpha%2B\frac{1}{2} \right) \right],](/2012-wikipedia_en_all_nopic_01_2012/I/b37c4f930a2d36e9f42be878ccbed396.png)
![L_n^{(\alpha)}(-x) \approx \frac{n^{\frac{\alpha}{2}-\frac{1}{4}}}{2\sqrt{\pi}} \frac{e^{-\frac{x}{2}}}{x^{\frac{\alpha}{2}%2B\frac{1}{4}}} \exp\left[2 \sqrt{x \left(n%2B\frac{\alpha%2B1}{2}\right)} \right],](/2012-wikipedia_en_all_nopic_01_2012/I/ba98efef8ef3c96be3510ad9caaf6019.png)
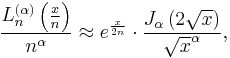
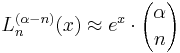
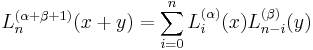
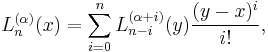
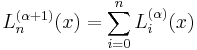
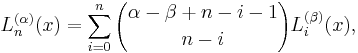
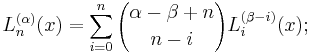
![\begin{align}L_n^{(\alpha)}(x)- \sum_{j=0}^{\Delta-1} {n%2B\alpha \choose n-j} (-1)^j \frac{x^j}{j!}&= (-1)^\Delta\frac{x^\Delta}{(\Delta-1)!} \sum_{i=0}^{n-\Delta} \frac{{n%2B\alpha \choose n-\Delta-i}}{(n-i){n \choose i}}L_i^{(\alpha%2B\Delta)}(x)\\[6pt]
&=(-1)^\Delta\frac{x^\Delta}{(\Delta-1)!} \sum_{i=0}^{n-\Delta} \frac{{n%2B\alpha-i-1 \choose n-\Delta-i}}{(n-i){n \choose i}}L_i^{(n%2B\alpha%2B\Delta-i)}(x).\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/d8ba5d3b9e8aecb5357b6329dae10c34.png)
![\begin{align}
L_n^{(\alpha)}(x) & = L_n^{(\alpha%2B1)}(x) - L_{n-1}^{(\alpha%2B1)}(x) = \sum_{j=0}^k {k \choose j} L_{n-j}^{(\alpha-k%2Bj)}(x), \\[10pt]
n L_n^{(\alpha)}(x) & = (n %2B \alpha )L_{n-1}^{(\alpha)}(x) - x L_{n-1}^{(\alpha%2B1)}(x), \\[10pt]
& \text{or } \frac{x^k}{k!}L_n^{(\alpha)}(x) = \sum_{i=0}^k (-1)^i {n%2Bi \choose i} {n%2B\alpha \choose k-i} L_{n%2Bi}^{(\alpha-k)}(x), \\[10pt]
n L_n^{(\alpha%2B1)}(x) & =(n-x) L_{n-1}^{(\alpha%2B1)}(x) %2B (n%2B\alpha)L_{n-1}^{(\alpha)}(x) \\[10pt]
x L_n^{(\alpha%2B1)}(x) & = (n%2B\alpha)L_{n-1}^{(\alpha)}(x)-(n-x)L_n^{(\alpha)}(x);
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/58781bec346a1073761ddde55f0ca531.png)
![\begin{align}L_n^{(\alpha)}(x)&= \left(2%2B\frac{\alpha-1-x}n \right) L_{n-1}^{(\alpha)}(x)- \left(1%2B\frac{\alpha-1}n \right) L_{n-2}^{(\alpha)}(x)\\[10pt]
&= \frac{\alpha%2B1-x}n L_{n-1}^{(\alpha%2B1)}(x)- \frac x n L_{n-2}^{(\alpha%2B2)}(x). \end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/b0c5ce0e0358c6c75a7a605925297c4f.png)
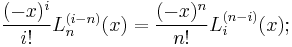
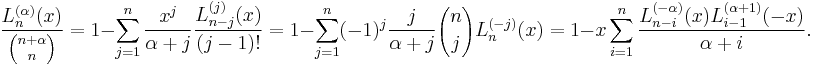
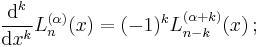
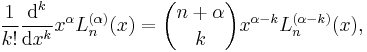
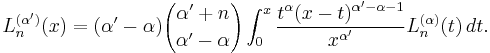
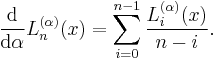
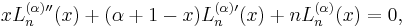
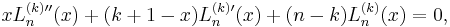
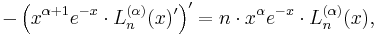
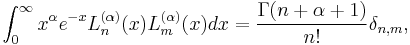
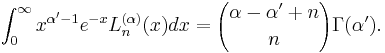
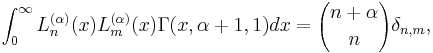
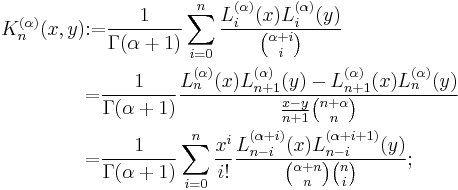
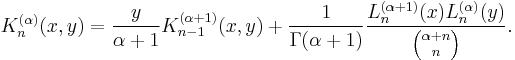
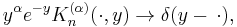
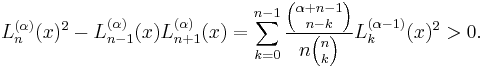
![\int_0^{\infty}x^{\alpha%2B1} e^{-x} \left[L_n^{(\alpha)}\right]^2 dx=
\frac{(n%2B\alpha)!}{n!}(2n%2B\alpha%2B1).](/2012-wikipedia_en_all_nopic_01_2012/I/171bd43c4b204e3a5de9c9a594f386e0.png)